Algorithm Design with python
Created Time: May 2, 2022 5:09 PM
Last Edited Time: May 2, 2022 7:18 PM
References: https://laboputer.github.io/ps/2018/01/03/exhaustive-search/
알고리즘 설계(Algorithm Design)
완전 탐색(Exhaustive Search)
완전 탐색= 모든 케이스 및 방법을 시도해보는것 = 무식하게푸는것
자주 등장하는 탐색유형
- 모든 순열 만들기(N!)
N개의 정점 간 거리가 주어지고, 어느순서가 가장빠를까?
중복불가 - 모든 조합 만들기(nCr)
N개의 숫자에서 숫자 2개의 합이 X인 방법의 수 - 모든 중복순열 만들기(N^r)
R개 보석의 부피와 가치가 주어질 떄, X부피의 가방에 보석을 담은 최대 가치는?
중복가능!
분할정복(Divide and Conquer)
어떤 문제를 작은 문제로 분할하고 풀고 이 부분 문제의 해를 통해 전체 문제의 해를 구하는것
- 문제를 둘 이상의 부분문제로 나눈다.
- 바로 해결가능한 아주 작은 부분 문제는 즉시 결과를 구한다. (N=0 or 1 등)
- 각 부분문제의 답을 이용하여 전체 문제의 답을 구한다.
재귀함수를 이용한다. =전체 문제의 답을 구하기 위해 부분문제의 답을 구하는구조
- 3^N을 구할때 3^(N/2) 를 2개곱하면 알수있고 계속 쪼개서 3^0=1에 도달…
동적계획법(Dynamic Programming)
동적계획법은 분할정복과 접근 방식이 유사하다. 어떤 문제를 작은 부분문제들로 나눠서 해결함
하지만, 분할 정복은 부분문제들을 한번만 구하면 되지만,동적계획법은 부분문제들이 여러번 사용되도록 문제를 분할합니다.
그래서 이미 해결한 부분문제들은 캐시 메모리에 넣어두고 이미 해결한 부분문제들의 해를 필요로 할때 사용됨.
동적계획법 적용조건(!)
- 최적부분구조
전체문제의 해를 부분문제들의 해만으로도 구할수있게 분할가능한 구조
A>C로가는 최단경로를 구할려면 A>B와 B>C를 합하면됨 - 중복되는 부분문제
전체문제를 해결함에 있어 똑같은 부분문제가 중복되어 발생하는 문제
이 두조건을 만족하면 다음과같이 동적계획법 이용하자
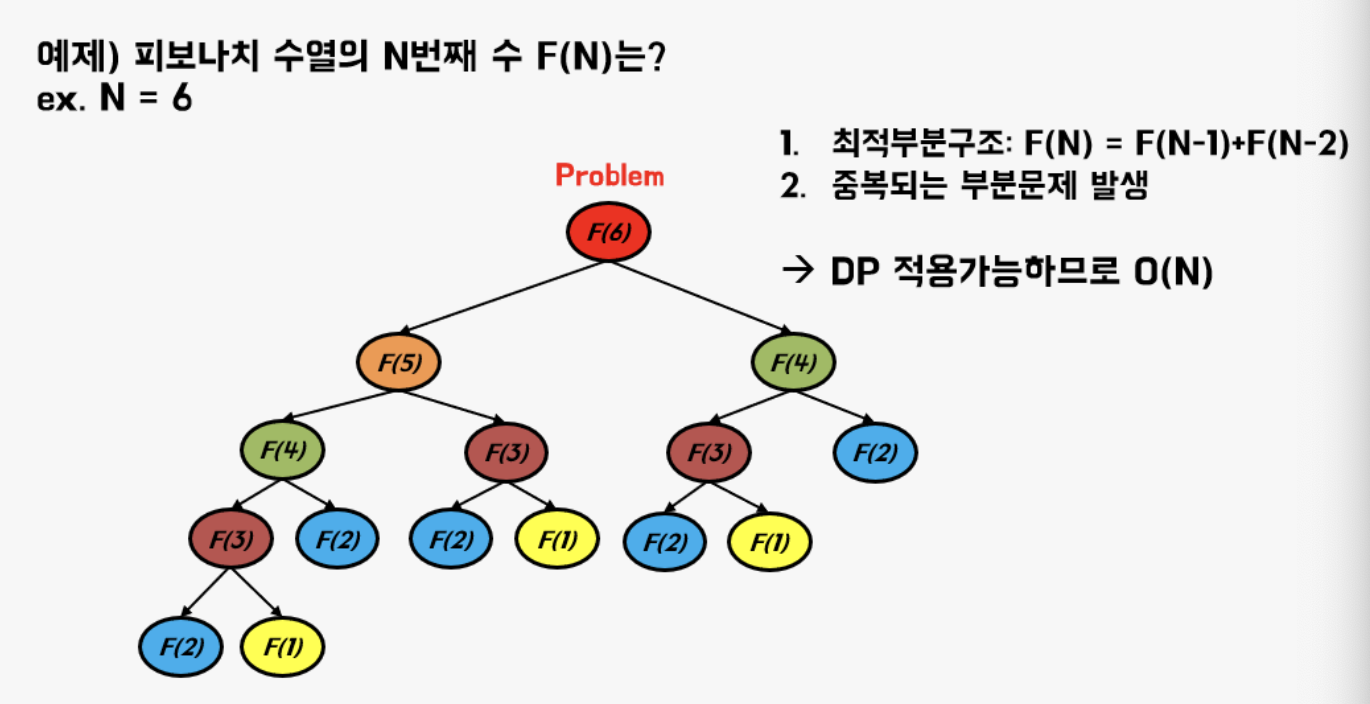
동적계획법 알고리즘
- 전체문제의 해가 부분문제의 해를 포함하도록 문제를 분할한다.
- 부분문제의 해를 구한 후 메모리에 저장한다(이미 구했다면 메모리의 값사용)
- 부분문제의 해를 이용해 전체문제의 해를 구한다.
탐욕법
완전탐색과 동적계획법처럼 모든 경우를 탐색하여 계산한 결과를 바탕으로 구하는 것이 아니라 매순간 가장 좋은 선택(지역적인 최적해)만 하는 것을 말한다.
근사해를 구할떄 유용하다!
탐욕법의 최적해 조건
- 최적부분구조
전체문제의 해를 부분문제들의 해만으로도 구할수있게 분할가능한구조 - 탐욕적 선택 속성
지역적인 최적의 선택이 전체문제의 해에 반드시 포함됨